Exercise
Last updated on 2024-11-12 | Edit this page
In this exercise, we will see how computational thinking can be used
to add up all the numbers between 1 and 200 in our heads,
i.e. 1 + 2 + 3 + 4 and so on. We should be able to do this
in less than a minute.
Seems impossible?
It’s not.
Using the first computational thinking step - Decomposition - we break the problem up into smaller pieces. Rather than trying to add the numbers up sequentially, which would be challenging for many people to do in their heads, let’s approach the task in a different way.
Decomposition
Let’s begin at each end of the 1-200 sequence by adding up the first and last numbers.
What is 200 + 1?
The answer is 201.
Decomposition (continued)
Let’s now add up the second and the second last numbers,
i.e. 199 + 2.
The answer is 201.
Decomposition (continued)
Let’s now add up the third and the third last numbers,
i.e. 198 + 3.
The answer is 201.
Pattern recognition
Using our second step - Pattern recognition - we should be
able to spot a clear pattern, i.e. that each pair of numbers appears to
add up to 201.
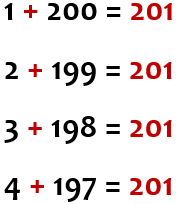
If we follow this same process with all the numbers
between 1 and 200, we will end up with 100 pairs, each
of which will add up to 201.
Algorithm
Using an Algorithm - another name for a series of steps - how do we calculate the final total?
We multiply the number of pairs (100) by
201 (the total to which each pair adds up).
100 * 201 gives us the answer of
20,100.
So far, so good.
Now, what about about our fourth step, Abstraction?
Abstraction
Abstraction will enable us to generalise from that experience, i.e. repeat the process we used to add up all the numbers between 1 and 200 to add up a different set of numbers, e.g., 1-500.
The Algorithm will be
(number to be added divided by 2) multiplied by
(number to be added +1). We can express that as an
algebraic formula:
(x/2) * (x + 1)
where x is the
number to be added.
That’s it! Using those four key steps, we have learned the basics of computational thinking.
Practice
Use the algorithm above to add up all the numbers between 1 and 24, 1 and 50, and 1 and 1,000.
Discussion
The numbers above are all even numbers. What would be the process for adding up numbers if the final number is an odd one, e.g., 17? Can you use the same formula? If not, what adaptations would you need to make to the formula?
